Det finns de som påstår att det är lätt att mäta kunskaper. Allt som oftast står det i tidningarna att elever får för höga betyg eller fel betyg med utgångspunkt i jämförelser mellan de betyg lärare har satt på elevernas kunskaper och elevers resultat på de nationella proven. Redan här förstår man kanske att det inte är helt lätt, för vem har egentligen mätt rätt? I dagsläget och på goda grunder som jag ska visa, ska emellertid inte de nationella proven styra lärares betyg. De ska vara ett stöd i betygssättningen. Anledningen är att det inte helt objektivt går att mäta den typ av kunskaper våra läroplaner anger att eleverna ska lära sig, och att mätandet i sig påverkar vad och hur eleverna lär sig. Detta brukar diskuteras i termer av validitet och reliabilitet. Validitet, giltighet, handlar ytterst om hur säkert vi kan uttala oss om ett resultat utifrån hur säkra vi är på vad vi har mätt, eller som Samuel Messick uttrycker det i sin klassiska artikel Validity:
Validity is an integrative evaluative judgment of the degree to which empirical evidence and theoretical rationales support the adequacy and appropriateness of inferences and actions based on test scores or other modes of assessment. (Messick 1989:13)
Messick diskuterar två hot mot möjligheten att göra valida tolkningar av ett testresultat, dels construct under representation, dels construct irrelevant variance. Det första handlar om att ett prov inte tillräckligt förmår fånga skillnaden mellan elever kring det vi ville mäta. Om vi t.ex. har ett flervalsprov i historia så fångar det elevernas skilda kunskaper kring historiska fakta men inte huruvida eleverna kan konstruera ett historiskt argument, eller för att ta något uppenbart, att muntlig förmåga inte mäts på ett skriftligt prov. Alltså, construct under representation handlar om att viktiga aspekter av ett kunnande är underrepresenterade i ett prov.
Construct irrelevant variance handlar om motsatsen, uppgiften mäter något som den inte borde mäta. I ett test i matematik kan frågorna vara formulerade med ett så pass svårt språk att vi inte vet om skillnaden mellan eleverna beror på läsfärdighet eller matematisk färdighet. Reliabilitet, trovärdighet, handlar om i vilken grad resultaten på ett test kan bero på slumpmässiga faktorer, eller faktorer utom testarens kontroll. Paul Black och Dylan Wiliam (2011) menar därför att reliabilitet ytterst är en fråga om construct irrelevant variance, alltså om validitet. Har ett test låg reliabilitet går det inte att göra valida tolkningar av resultatet eftersom man inte vet vad resultatet beror på.
En vanlig metafor för reliabilitet och validitet är nedanstående bild (se t.ex. Koretz 2008):
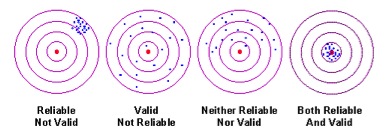
Den fjärde bilden ses som både reliabel och valid. Men säg nu att kursplanen definierar hela tavlan som mål för undervisningen. Då får du en påtaglig construct under representation i det fjärde fallet. Snarast är det då den andra bilden som ger bäst construct representation, men mot en betydligt lägre inre konsistens. Man får alltså i praktiken i viss utsträckning bestämma sig för om man ska betona reliabilitet eller validitet, eller hitta någon lämplig kompromiss – vilket inte är det lättaste.
Det finns tre övergripande hot mot reliabiliteten:
1) Olika bedömare gör olika tolkningar av elevernas svar
2) Elevernas dagsform påverkar hur de svarar och om de kan eller inte
3) Olika uppgifter men som mäter samma kunskaper uppfattas på olika sätt av olika elever.
Ett sätt att öka reliabiliteten är genom att införa fler frågor på varje mätområde. Vi vill kanske ge eleverna tre olika möjligheter att visa att de förstår ett specifikt moment. Om vi på detta sätt vill öka den så kallad interbedömarreliabiliteten från ett läge där oberoende bedömare kommer till samma slutsatser i 64 procent av fallen till 81 procent av fallen, behövs en uppgiftsmängd som förlänger provtiden 5 till 6 gånger menar Black och Wiliam (2011), dvs. upp mot 25-30 timmar om vi tar ett Nationellt prov som exempel. Skulle vi göra det får vi dock ett annat problem – eleverna blir så trötta att de underpresterar. Alternativet är att vi gör ett test som täcker in färre områden, men då får vi alltså underrepresenterade kunskapsområden. Det hela handlar om klassisk testteori. Vanligtvis brukar man beräkna hur många uppgifter som behöver adderas till ett prov för att uppnå en viss reliabilitet. Det gör man med hjälp av Spearman-Browns formel. De flesta provkonstruktörer väljer en balans mellan dessa poler med den uppenbara konsekvensen att det finns mätfel även i de allra mest ambitiöst konstruerade proven. Ska man göra vettiga tolkningar av ett prov måste man därför ha en aning om mätfelets storlek. Black och Wiliam (2011) har ett resonemang om hur man kan tänka om det genom att ha en hypotes om elevernas rätta resultat. Det finns inget meningsfullt prov där elever skulle få samma resultat varje gång. Elever gör olika fel vid varje mättillfälle och bedömare gör olika rättningar vid olika tillfällen. Men om man lade ihop en elevs resultat på fem till sex liknande prov under en begränsad tid skulle man få fram ett genomsnittligt resultat som kallas the true score – det rätta resultatet. Ett sätt att åstadkomma detta i praktiken är att arbeta med split half-metoden som innebär att man gör ett prov som kan delas i två delar. Sedan jämför man utfallet på de två delarna. Är det hög överensstämmelse har uppgifterna en hög inre konsistens avseende vad de mäter. Överensstämmelsen är dock också beroende av hur man delar upp testet och därför måste man korrelera alla tänkbara rimliga sätt att dela testet på med varandra. Då får man ett värde som kallas Cronbachs alpha och som uttrycks mellan 0 och 1, där 0 betyder att proven ger slumpmässiga utfall och 1 att provet är helt reliabelt – varje gång vi gör det får vi samma resultat. En vanlig uppfattning är att Cronbach alpha bör ligga på 0.7 och uppåt om testet ska vara användbart, men det beror givetvis på vad det faktiskt är man mäter. För att förstå vilken effekt olika grader av reliabilitet faktiskt kan få t.ex. för vilket provbetyg en elev får behöver vi kombinera Cronbach alpha med ett mått på elevens sanna resultat (the true score).
För att undersöka hur provets inre konsistens påverkar resultatet för en elev kan Cronbach alpha sättas i relation till standardavvikelsen, dvs. den genomsnittliga avvikelsen från medelvärdet. En bra illustration till hur man kan räkna finns i Black och Wiliam (2011). På en normalfördelningskurva faller 68 procent av resultaten inom en standardavvikelse och 96 procent inom två standardavvikelser. Genom att kombinera dessa mått går det att få fram ett förväntat standardfel, SEM. Standardfelet anger för varje reliabilitetsnivå den förväntade spridningen av felprocent inom en och samma faktiska kunskapsmängd.
Formeln för SEM är X √(1-r)
Om r är reliabilitet så betyder detta att SEM på ett prov med en reliabilitet på 0.85, där man kan få 50 poäng och där standardavvikelsen (X) är 7,5 poäng blir 2,9 poäng (SEM=7,5√(1-0,85)=2,9). Det innebär att den ”sanna poängen” för en elev med 35 provpoäng till 68 procents sannolikhet ligger mellan 32 och 38 poäng. Vill man ha 95 procents säkerhet kan man säga att den ligger mellan 29 och 41. Detta är i själva verket en approximation, men används allmänt i professionell provanalys. Detta innebär hursomhelst att i en klass på 30 elever så är det minst en elev, vi vet aldrig vem, som avviker mer en 12 procent i positiv eller negativ riktning, det kan vi heller inte veta, från sitt riktiga resultat. Minst tio elever avviker 6 procent från sitt sanna resultat relaterat till provens bristande inre konsistens (som i det här exemplet trots allt inte var så farligt hög). Effekten för den enskilda individen kan dock bli stor varför professionella testkonstruktörer gärna är extra försiktiga med vilka slutsatser de drar från ett prov. Black och Wiliam skriver:
even the best tests can be widly inaccurate for a few individual students /…/ This is why testing experts invariably say that high-stakes decisions should never be based solely on the results of a single test. (Black & Wiliam 2011, s. 252)
Det är också av detta och likande skäl som nationella prov inte ska styra elevernas betyg. Om de gör det kommer vissa elever ändå att få fel betyg. Staten har därför valt att lita också på lärarnas omdömen. Frågan som uppstår är emellertid om lärares betyg hamnar ännu mer fel. Det kan vi inte veta med mindre än att vi forskar mer om hur lärare tänker när de ger eleverna deras betyg. Vi vet alltså inte vilken bedömning det är som är mest construct relevant, provbetyget eller lärarnas betyg. Men om vi bara håller oss till reliabiliteten i bedömningarna av proven går den att förbättra med olika medel. Ett sätt har varit att erbjuda elevexempel för olika betygsnivåer så att lärarna vet vad de ska titta efter. Det kvarstår dock fortfarande en stor del bristande bedömaröverensstämmelse, särskilt i uppsatsdelarna. Ett rimligt nästa steg är att låta lärare rätta proven tillsammans i grupp. Man rättar alltså sina egna elevers resultat och de andra lärarnas gemensamt. Det skulle göra att lärarna ”skrapar av” varandras extremer och därigenom, om gruppen är någorlunda heterogen, men inte nödvändigtvis större än 4-5 lärare, når en norm som skulle likna den liknande grupper skulle komma fram till (för en bra beskrivning av hur det praktiskt kan gå till se här och här). Det krävs alltså inte en särskilt stor kritisk massa för att enas om den mest rimliga tolkningen. I en sådan process skulle lärarna också utveckla sin ämneskompetens i det att de lära av varandra vad som är viktigt att fästa uppmärksamhet vid i olika moment av ämnet. Att låta lärare kontrollrätta varandras elevers anonymiserade prov menar jag däremot är en sämre väg att gå. Det förstärker misstroendet till lärarna och det blir inte nödvändigtvis rättvisare för eleven. Framförallt tar det bort ett tillfälle för lärare att lära av varandra. Bedömning av elevers kunskaper kan aldrig ske helt objektivt – däremot kan det utföras med en tillräckligt hög grad av intersubjektivitet för att tillfredsställa både individens och samhällets krav på likvärdighet!
Referenser
Black, Paul and Wiliam, Dylan (2011). The reliability of assessments. In John Gardner (ed.). Assessment and Learning. 2nd edition Los Angeles and London: Sage Publications, p. 243–263.
Koretz, Daniel M. (2008). Measuring up: what educational testing really tells us. Cambridge, Mass.: Harvard University Press
Messick, Samuel (1989). Validity. In Robert L. Linn (ed.): Educational Measurement. 3d edition 1993. Phoenix: The Oryx Press, p. 13–103.